Vytváření virtuálních 3D modelů tento pracovní rámec pojímá jako sled elementárních operací, vepsaných do Python kódu. Interaktivní modelování, kdy se používají nástroje aplikace, může být zábava, ale většinou jen do okamžiku, kdy je potřeba podobné operace opakovat pořád dokola. Pak je výhodnější operace zaznamenat do "makra". Sled operací kreslící program zaznamená a následně je můžeme aplikovat. Tato možnost má své nevýhody. Jsme odkázáni na způsob, jak kreslící program s makry zachází, jak je můžeme upravovat a jak jsou pro nás jejich kódy srozumitelné. Protože nejsme dokonalí, děláme chyby i při kreslení modelu, avšak jde-li o chybu, kterou lze lehce opravit interaktivním zásahem, není to problém. Pokud je však chyba v celkové koncepci návrhu, je její náprava pracná. Často pak, ve snaze si práci ulehčit, budeme chyby opravovat dalšími chybami, "vytloukat klíny klínem", až se spokojíme s nedokonalým výsledkem. Proč tedy nedefinovat něco podobného makrům, ale mnohem přehledněji pod naší kontrolou už od samého začátku návrhu? Budeme-li mít celý proces definovaný metodicky a kompletně v kódu, nebude problém kterékoli pravidlo poupravit a nechat program provést celou práci od začátku až do konce za nás. Chyba již nebude chybou, ale jen špatným pravidlem, které napravíme v zárodku a hlavně kdykoli. Budeme mít téměř neomezené možnosti optimalizací a tvorby vlastních metod, než když jsme odkázáni pouze na interaktivní metodiku kreslícího programu. Pro větší názornost je zde uveden jeden z příkladů, jak vygenerovat požadovaný model kompletně jen pomocí kódu prostřednictvím aplikace FreeCAD:

demo0.py (stáhnout)

Příklad demo0.py je nutné spolu s moduly tree.py, freeCADTree.py a piping.py (demo0.zip) umístit do složky, kde FreeCAD moduly očekává. To je možné zjistit ve FreeCADu: "Makro -> Makra -> Umístění uživatelských maker:". Na Linuxu to bude něco podobného jako ~/.local/share/FreeCAD/Macro. Ve Windows: C:\Users\<Uživatel>\AppData\Roaming\FreeCAD\Macro.

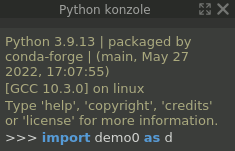
Příklad spustíme jako import modulu příkazem import demo0 as d z "Python konzole" panelu aplikace FreeCAD. Pokud není panel zobrazen, zobrazit jej můžeme: "Zobrazit -> Panely -> Python konzole". Modul vygeneruje požadované objekty a vloží je do nového dokumentu FreeCADu, který sám vytvoří.

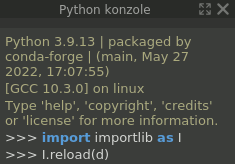
import importlib as I
I.reload(d) # z Python konzole

Pro opakované provedení je nutné provést příkazy import importlib as I a I.reload(d). To je potřeba například po úpravě moduluu (textovým editorem), nebo potřebě nový dokument opět vygenerovat.

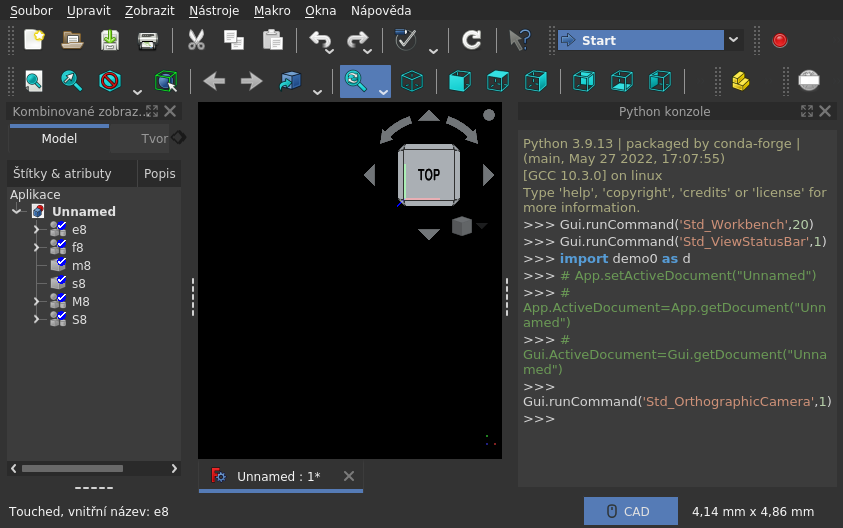
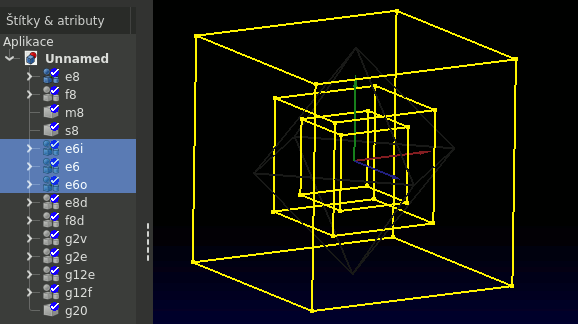
Struktury vygenerované do dokumentu:

e8: hrany fazet v kontextu oktantu (fazety) a 3D osy, na které leží první vrchol (druhý je na následující 3D ose) - ideální podklad pro další konstrukce; jedná se prakticky o osmistěn
f8: fazety vzniklé vždy z 3 hran
m8: síť z hran - kostra osmistěnu; již bez "xyzd" kontextu a duplicit - podklad pro další konstrukce, vycházející z tohoto tvaru
s8: těleso z fazet - osmistěn s plnými stěnami
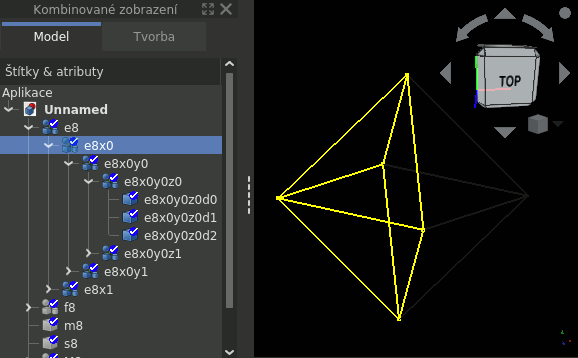
M8: ztělesněné komponenty tvaru m8 - obalené hmotou o poloměru J.r; z fazet jsou hranoly, z hran trubky a z uzlů koule
S8: --||-- s8 --||--

Všechny tyto struktury budou viditelné v panelu "Kombinované zobrazení - Model" (klik na jméno, mezerník), ale i jako atributy modulu, přístupné z panelu "Python konzole", kam stačí napsat název atributu (např. d.e8 nebo d.f8). Z konzole jsou přístupné i všechny ostatní atributy modulu, které nemají alternativu v dokumentu (např. d.o8 nebo d.c8 atd.). Objekty, které jsou přístupné interaktivně i z konzole, lze jednoduše zkoumat v každém aspektu, především jako nativní objekty, které FreeCAD a integrované moduly nabízí.

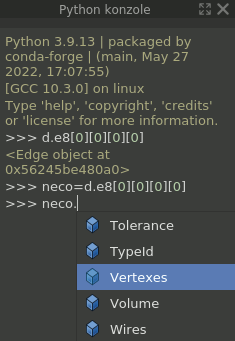
vobrazení atributů objektu v Python konzoli

Stačí za název atributu napsat tečku a konzole nabídne všechny atributy objektu, včetně metod, které lze v konzoli okamžitě použít - spustit jako příkaz Pythonu. Ostatně tak lze interaktivně zkoumat veškeré objekty obsažené v aplikaci nebo dokumentu. Pro prozkoumání z konzole bude patrně nejzajímavější série pomocných struktur, předcházející struktuře e8, které do dokumentu vkládány nejsou, protože jde o pouhé body. To jsou atributy pl, o8, c8, v8, vr8, vv8, popsané v komentářích přímo v modulu.

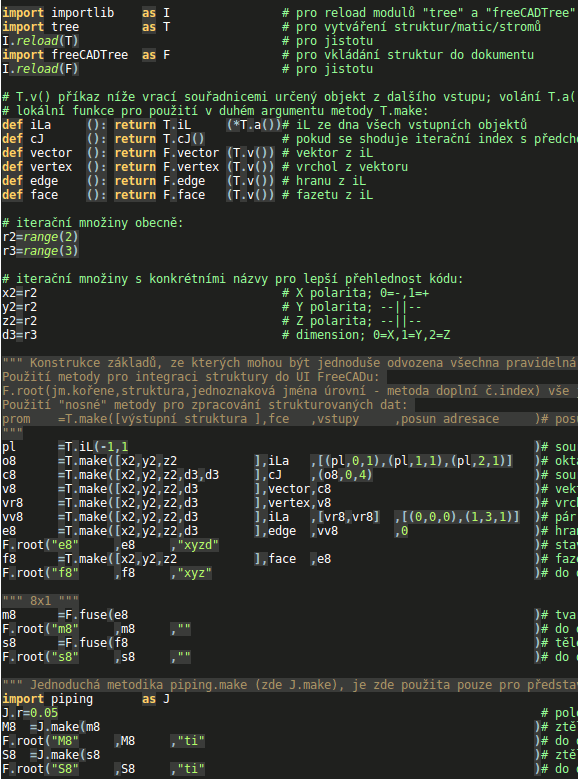
náhled souboru demo0.py v textovém heditoru Geany

Příklad demonstruje kompletní proces generování FreeCAD dokumentu se všemi kroky, jejichž výsledky jsou přístupné skrze atributy modulu, aby bylo možné celý proces zkoumat a případně hledat chyby. Psaní podobného kódu probíhá tak, že jsou postupně přidávány elementární operace nad celými strukturami objektů, až je dosaženo cíle. Vývoj 3D modelu může působit zpočátku složitě, ale po osvojení metodiky pracovního rámce to může být mnohem větší "zábava", než jen interaktivní modelování, protože modelář se stává zároveň programátorem a metodikem. Frustrace z případných chyb na 3D modelu zcela odpadá, protože je lze odstranit jen změnou metodiky, kterou má vývojář plně pod kontrolou. Příklad by měl správně končit vytvořením struktury e8, protože dále může být použita v několika scénářích, z nichž nejzajímavější bude patrně odvozování dalších geometrických struktur.

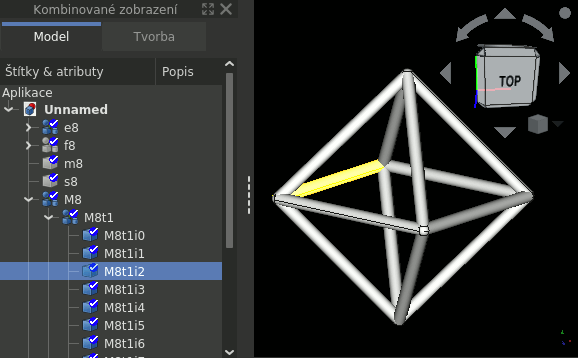
Struktury M8 a S8 slouží jen k demonstraci nějakého jednoduchého, ale názorného výsledku všech operací. Sloučením všech komponent (např. fM8=F.fuse(M8)) bychom již dostali použitelné těleso a pokud bychom je chtěli použít i interaktivně, mohli bychom je umístit do dokumentu FreeCADu dalším příkazem F.root("fM8",fM8,"").

V příkladu je importován standardní modul importlib, který je součástí distribuce Pythonu a je použit jen pro znovunačtení modulů, které mají stavová data. Importovány jsou i tři moduly z vlastní dílny, které navazují na moduly "FreeCAD" balíku a přidávají metodiku pracovního rámce:

tree.py

Definuje objekt iL, rozšiřující nativní objekt list a přidává další metodiku pracující se stromovými strukturami.

Nejpoužívanější je jeho metoda make, která zpracovává vstupní struktury a vytváří struktury výstupní. Vstupní i výstupní struktury se podobají maticím, proto je použití metody někdy zjednodušeně nazýváno "maticovou" operací. Pro pochopení použití metody je vhodné příklad otevřít v jiném okně, ideálně v textovém editoru. Pokud soubory rozbalíme do adresáře, kde FreeCAD hledá moduly (viz první odstavec pod titulkem "demo0.py"), můžeme vše hned zkoušet v praxi. Dále popsané případy najdeme v souboru demo0.py u T.make příkazů.

Rozměry výstupní struktury/matice definuje první argument, podle kterého také probíhají iterace při počítání jejích hodnot. Hodnoty se počítají metodou uvedenou v druhém argumentu. Vstupní struktury/matice jsou uvedeny v třetím argumentu. Pokud je použito více struktur, než jen jedna, je nutné uvést seznam, například [pl,pl,pl]. Má-li vstupní struktura/matice jiné rozměry než výstupní, je nutné uvést které. K tomu je potřeba jednotlivé vstupy ještě "zabalit" do "tuple" kulatých závorek, kde první prvek uvádí vlastní vsupní strukturu, druhý uvádí číslo rozměru a třetí počet rozměrů, kterými se má struktura adresovat. Například definice (pl,0,1) říká, že ze struktury pl se mají použít hodnoty adresované souřadnicí nultého rozměru a jen tohoto jednoho. Čtrvrtý argument definuje posun adresace vstupní hodnoty v matici. To je užitečné, máme-li dvě vstupní struktury/matice a pro výpočet výstupní hodnoty potřebujeme z každé z nich hodnotu na jiné souřadnici. Posun je nutné uvést jako relativní vzhledem k výstupnímu rozměru. Například argument [(0,0,0),(1,3,1)] říká, že první vstupní matice se má použít standardně (jen syntaktická výplň), ale u druhé se má u třetího rozměru posunout souřadnice +1. A má to platit jen pro tento jeden rozměr (říká poslední číslice 1 v tuple). Třetí, čtvrtý a pátý (v příkladu nepoužit) argument metody make má stejnou syntaxi. Pokud má jeho hodnota platit pro všechny rozměry, uvádí se přímo. Potřebujeme-li hodnotu použít jen pro některé rozměry, je nutné argument ještě zabalit do kulatých závorek a uvést hodnotu, čárku, číslo rozměru, čárku a počet rozměrů, pro které má hodnota platit.

freeCADTree.py

Tvoří rozhraní mezi nativními moduly a vlastní metodikou nebo dalšími vlastními moduly pracovního rámce. Vlastní metodika slouží především k integraci vytvářených struktur do dokumentů aplikace FreeCAD. Po jeho importu příkazem import FreeCADTree as F (v příkladu nahoře) můžeme například nastavit jeho atribut F.Vi=True, který říká, že metoda F.root bude do dokumentu vkládat objekty jako viditelné. Výchozí hodnoda je False.

piping.py

Velice jednoduchý modul sloužící jen k "obalování" elementárních tvarů hmotou metodou make. Metoda vezme všechny fazety, hrany i vrcholy určeného tvaru a "obalí je" hmotou o poloměru nastaveném v atributu r. Metoda vrátí strukturu tří seznamů: hranolů z fazet, válců z hran a koulí z vrcholů. Pokud budeme chtít sloučit všechna tato tělesa do jednoho, můžeme k tomu jednoduše použít fuse metodu modulu freeCADTree.

demo1.py (stáhnout)

Další příklad navazuje na demo0.py. Přidává kód, který z připravených struktur odvozuje struktury další, důsledně zachovávající kontext stavby. Konkrétně jde o konstrukční prvky duálního tělesa k osmistěnu, kterým je šestistěn - krychle. Obecně - duální těleso je možné jednoduše odvodit ze středů stěn tělesa původního, kam umístíme vrcholy tělesa duálního. Přitom není nutné dodržet přesnou délku vektoru, ale postačí jen jeho směr. Na tuto "vektorovou" přímku pak můžeme umístit vrchol vzdálený od středu tělesa přesně podle toho, jak velké má duální těleso být. Pokud vrcholy ponecháme stejně vzdálené, jako stěny tělesa původního, bude duální těleso jemu vepsané. Vrcholy duálního tělesa je možné umístit i do takové vzdálenosti od středu, že jejich spojnice/hrany budou pravoúhle protínat hrany tělesa původního. Z takto spojené sítě hran je pak možné generovat "trubkovou stavebnici", která již bude obsahovat tělesa obě. Výpočet velikosti duálního tělesa a jeho konstrukce je obsažena v tomto příkladu. Zároveň je v příkladu demo1.py oproti demo0.py i nekolik funkcí a detailů navíc. Po stažení (demo1.zip) je potřeba archiv rozbalit do adresáře zmíněného u předchozího příkladu.

demo2.py (stáhnout)

V příkladu demo2.py je postup odvození dvacetistěnu z konstrukčních prvků osmistěnu.

Konstrukce dvacetistěnu

Jedná se pravděpodobně o nejpraktičtější příklad použití metodiky pracovního rámce, pokud jde o konstrukci pravidelných těles. Dvacetistěn je možné považovat za nejzajímavější základ pro složitější tvary. Můžeme jej nazývat tělesem "zlatého poměru", nebo zkráceně "zlatým tělesem". K jeho sestrojení je toto číslo přímo nezbytné.

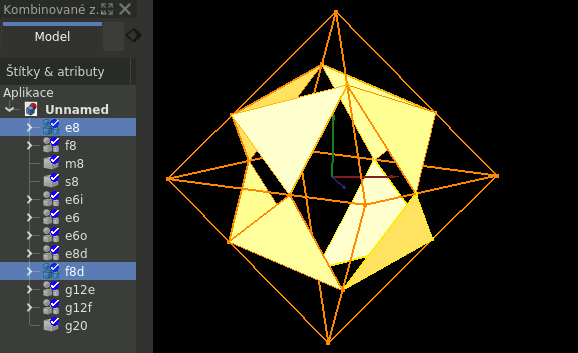
Pokud vyjdeme z osmistěnu, můžeme dvacetistěn do něj jednoduše vepsat, protože osm stěn z dvaceti leží ve stejných rovinách - uvnitř stěn osmistěnu. Osmistěn je ztělesněním absolutní adresace oktantů, kterými jsou jeho stěny na těchto rovinách vymezeny pouhým umístěním vrcholů na souřadné osy symetricky podle bodu nula (0,0,0). Stěny dvacetistěnu jsou oproti těm osmistěnovým pouze pootočeny tak, že jejich vrcholy dělí hrany stěn osmistěnu na dvě části, přesně ve "zlatém poměru" jejich délek. Tímto okrajováním stěn osmistěnu na "oktantové" stěny dvacetistěnu (adresované absolutně) dostaneme základ, tedy všechny vrcholy dvacetistěnu v kontextu oktantů. Vrcholy dvacetistěnu, krom toho, že ve zlatém poměru dělí hrany osmistěnu, jsou zároveň vrcholy tří obdélníhových (2D) "zlatých" stránek. Tyto tři 2D "zlaté" (poměrem délek stran) stránky jsou položeny na "nulové" roviny "souřadného systému" tak, že se vzájemně protínají. Základních osm "absolutních - oktantových" stěn dvacetistěnu je k dokonalosti ještě nutné doplnit dvanácti "relativními - kvadrantovými" stěnami. Ty jsou, jak je zmíněno, adresovány k 3D rozměru relativně. K uzavření jejich trojúhelníkového tvaru je nutné přidat kratší hrany 2D "zlatých stránek" se stejnou adresací.

"Oktantové" stěny lze doplnit "12-ti relativními" i jiným způsobem. Můžeme k tomu použít, namísto těch kratších, pro změnu delší hrany 2D "zlatých stránek". Ty je pak možné použít například jako pevné části tenzegritní konstrukce, kde hrany základních "oktantových" stěn dvacetistěnu tvoří napružená vlákna.

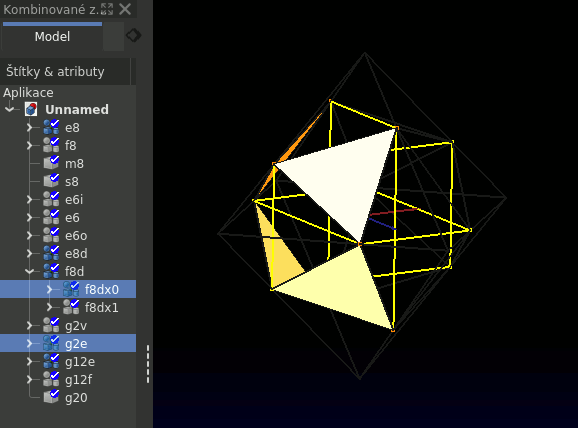
Absolutní adresace

Nultý index vyjadřuje "duant" (poloprostor) půlící prostor v ose X, první index "duant" půlící v ose Y a třetí půlící v ose Z. V kontextu předchozích indexů to je duant X, kvadrant XY a oktant XYZ. Následuje index vyjadřující relativní 3D rozměr. Ve struktuře e8d určují první 3 indexy oktant, do kterého je umístěna stěna. Poslední index určuje stranu (hranu) stěny. Ukázáním na odpovídající složky objektů ve FreeCAD dokumentu, nebo z "Python konzole" je vše dobře patrné:

gvr8: vrchol dělící hranu osmistěnu zlatým řezem
gvv8: pár vrcholů stěny dvacetistěnu pro hranu
e8d: hrana stěny v kontextu oktantu a 3D rozměru - ideální podklad pro další konstrukce
f8d: stěna v kontextu oktantu a 3D rozměru

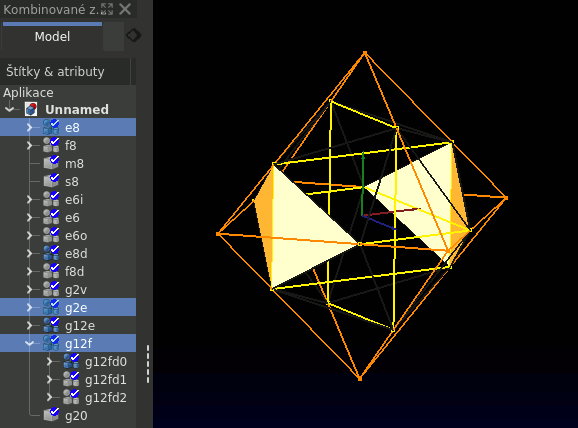
Přeadresování

Ve struktuře e8d jsou stěny adresovány absolutně. K vytvoření těchto stěn byly použity, podobně jako u osmistěnu, tři hrany - pro každý 3D rozměr jedna. Aby bylo možné doplnit základních osm stěn dalšími dvanácti, je nutné doplnit i 12 hran k 24 již vytvořeným. 12 nových hran vychází z konstrukce "tří zlatých stránek". Jsou to jejich kratších hrany. Proto je nutné absolutní adresaci dvojic hran, které jimi mají být doplněny na kompletní stěny, transformovat na adresaci relativní. To je provedeno operacemi vi1320 a vi0 (viz příklad).

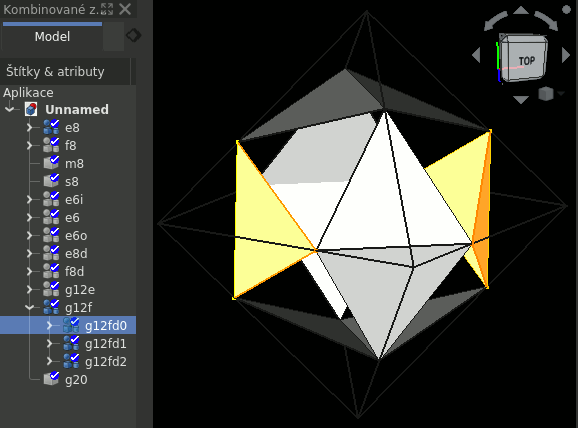
Relativní adresace

Tato adresace začíná (nultý index) 3D rozměrem (souřadnou osou/rovinou). Další indexy jsou pak relativní k nultému, ale dělení na "duant", kvadrant a oktant vyjadřují také. Relativně jsou adresovány struktury:

g12vr: jeden vrchol hrany z "oktantové stěny"
g12e1: spojení těchto vrcholů - jsou to zároveň vrcholy "zlatých" stránek
g12e: hrana stěny v jedné struktuře (dvě z neúplné stěny a jedna ze "zlaté stránky" - ta kratší)
g12f: stěna z hran

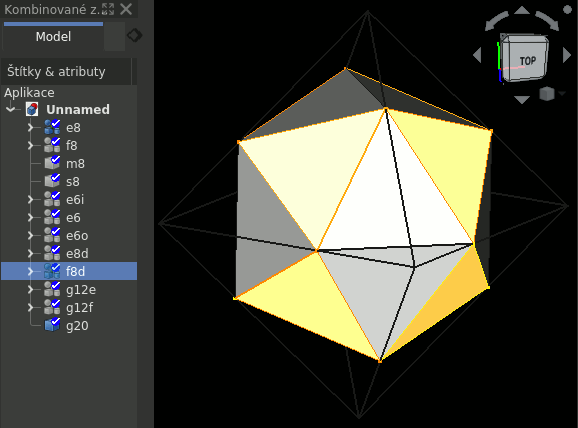
Finální tvar vznikne spojením všech stěn do jedné struktury g20. Po stažení (demo2.zip) je potřeba archiv rozbalit do adresáře zmíněného na začátku článku.

Real Mesh Materializer